Egwald Mathematics: Space Curves

by

Elmer G. Wiens

Egwald's popular web pages are provided without cost to users.
Please show your support by joining Egwald Web Services as a Facebook Fan:
Follow Elmer Wiens on Twitter:

Space Curves

Suppose that the location of the point P(x,y,z) in three dimensional space is determined as a function of time t. Specifically, suppose that:

x = x(t),   y = y(t),   z = z(t)

Thus, each component of P is a separate function of time. Then as t varies, the locus of P is a curve in three dimensional space.

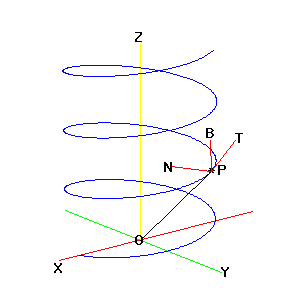
For example, the following equations will trace a circular helix.

x = a * cos(w * t),   y = b * sin(w * t),   z = c * t

In the example to the right, a = 1.5, b = 1.5, c = .1, w = pi/6, 0 < t < 40 T = the tangent to the curve at P with t = 16 N = the normal to the curve at P B is perpendicular to T and N B = T X N, where X denotes cross product The system of mutually orthogonal vectors, T, N, and B, is used extensively in analyzing space curves in general.

Let the vector from the origin to the point P be R. Let s be the arc length along the space curve from P to another point P₀. Then

R = i * x(t) + j * y(t) + k * z(t)

where i, j, and k are the unit vectors along the x, y, and z axis, respectively.

For a circular helix:

R = i * a * cos(w * t) + j * b * sin(w * t) + k * c * t

To obtain the unit tangent vector, T, to the space curve at P, differentiate R with respect to s:

T = dR / ds = { i*(-a*w*sin(w*t) + j*(b*w*cos(w*t)) + k*c } dt / ds

For T to be a unit vector requires that the magnitude of T be 1. So,

dt / ds = 1 / sqrt[w² * (a² * sin²(w*t) + b² * cos²(w*t)) + c²] = kap.

To obtain the unit normal vector, N, to the space curve at P, differentiate T with respect to s, dT / ds = kappa * N, with |N| = 1.

dT / ds = (dT/dt)/(dt/ds) = kap * { i*(a*w²*cos(w*t) + j*(b*w²(sin(w*t))} * dt / ds

|dT/ds| = kappa = kap² * w² * sqrt[ a²*cos²(w*t) + b² * sin²(w*t)]

Kappa is the curvature of the space curve at P.

Notes:
1. The velocity vector, V(t) = dR / dt, in the direction of T, is given by

V = dR / dt = i*(-a*w*sin(w*t) + j*(b*w*cos(w*t)) + k*c.

2. The acceleration vector, A(t) = dV / dt is given by

A = dT / dt = i*(a*w²*cos(w*t) + j*(b*w²(sin(w*t)).

3. When a = b, matters simplify because cos²(w*t) + sin²(w*t) = 1. Then

Space Curves - Helix Reset value of a [.5, 2.5] x = a * cos(w*t) 2 Reset value of b [.5, 2.5] y = b * cos(w*t) 1.5 Reset value of c [.05, .5] z = c * t 0.1