Egwald Mathematics: Geometry - Trajectory of a Projectiles

by

Elmer G. Wiens

Egwald's popular web pages are provided without cost to users.
Please show your support by joining Egwald Web Services as a Facebook Fan:
Follow Elmer Wiens on Twitter:

A projectile is fired from a gun that is mounted on a cliff above the sea. What is the range of the gun? At what angle should the gun be fired to hit a ship within its range? z0 = height of the gun above the x-y plane. v0 = muzzle velocity = initial velocity of the projectile. alpha = the angle between the horizontal (the x-y plane) and the muzzle of the gun. z(t) = the height of the projectile t seconds after being fired. r(t) = the distance of the projectile from the gun after t seconds. g = pull of gravity. Then the parametric equations of motion of (r(t), z(t)) are: r(t) = v0 * cos(alpha) * t z(t) = -1/2 * g * t^2 + v0 * sin(alpha) * t + z0
The trajectory of the particle for varying angles alpha.
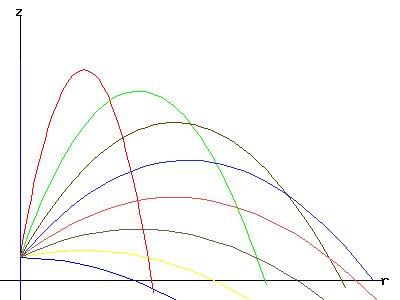
The trajectory of the particle in varying directions.

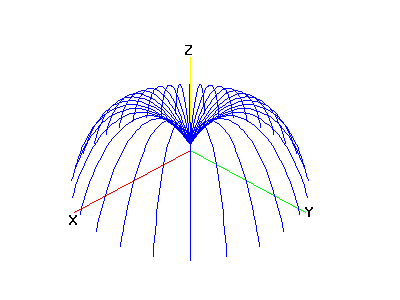
Change the angle alpha (in radians, try .75) and click "Submit" to view the trajectories of the particle at the new angle.