|
Egwald Mathematics: Hyperbolic Functions
by
Elmer G. Wiens
Egwald's popular web pages are provided without cost to users.
Please show your support by joining Egwald Web Services as a Facebook Fan:
Follow Elmer Wiens on Twitter:
Hyperbolic Functions
The hyperbolic functions are very useful in solving many engineering problems. While their names resemble the natural trigonometric functions, they are not periodic like the trig. functions. The hyperbolic functions are based on the exponential function, which is definitely not periodic.
| hyperbolic cosine: | cosh(u) = .5 * (eu + e-u) |
hyperbolic sine: | sinh(u) = .5 * (eu - e-u) |
| hyperbolic tangent: | tanh(u) = sinh(u) / cosh(u) |
hyperbolic cotangent: | coth(u) = cosh(u) / sinh(u) |
| hyperbolic secant: | sech(u) = 1 / cosh(u) |
hyperbolic cosecant: | csch(u) = 1 / sinh(u) |
As u goes from -infinity to +infinity, the point (x, y) = (cosh(u),sinh(u)) traces out the unit hyperbola:
x^2 - y^2 = 1
as, cosh2(u) - sinh2(u) = 1
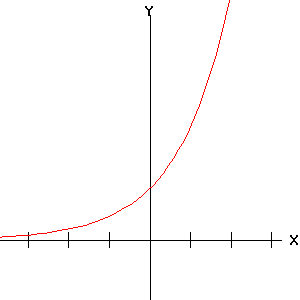
| y = ex | x = cosh(u), y = sinh(u) |
|---|
|
|
|
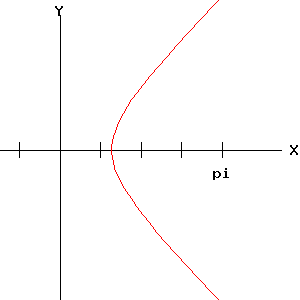
