|
Egwald Mathematics: Linear Algebra
Systems of Linear Differential Equations
Stability Analysis
by
Elmer G. Wiens
Linear Systems
The simplest two dimensional, continuous time process is the second order, linear homogeneous system with constant coefficients:
dx1 / dt = a * x1 + b * x2,
dx2 / dt = c * x1 + d * x2
Let the matrix A be:
and the column vectors x and dx / dt be:
xT = (x1, x2),
dxT / dt = ( dx1 / dt, dx2 / dt ),
where "T" indicates the transpose of the vector from a column vector to a row vector.
The linear system has the form:
dx / dt = A * x. (2)
The origin, oT = (0, 0), is an equilibrium (fixed) point of (2) because A * o = o.
The general 2 by 2 matrix, A, has:
p = trace(A) = a + d, and
q = det(A) = a*d - b*c.
Its characteristic equations is:
f(µ) = µ2 - p * µ + q
Factoring this quadratic equation yields the pair of eigenvalues, µ1 and µ2, where:
µ1 = { p + sqrt(p2 - 4 * q) } / 2 , and
µ2 = { p - sqrt(p2 - 4 * q) } / 2.
Moreover:
p = µ1 + µ2,
q = µ1 * µ2.
Designate the discriminant of the characteristic equation by:
d = p2 - 4 * q.
Classification of Fixed Points
The following diagram classifies the fixed points (critical points) of the linear system (2) according to the values of p = trace(A), q = det(A), and d = disc(A). The parabola, p2 - 4 * q = 0, is the locus of points (p, q) for which d = 0.
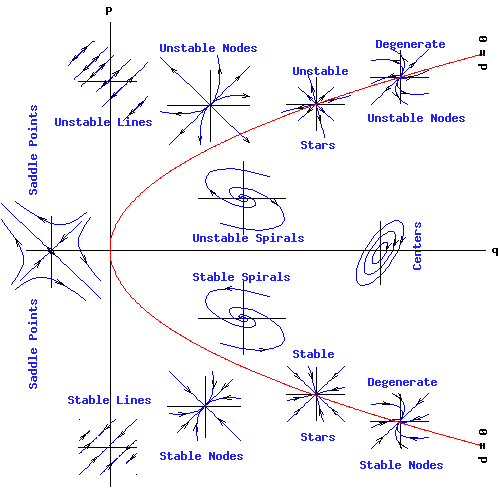
In the region of the (q, p) plain enclosed by the parabola, p2 - 4 * q, the eigenvalues µ1 and µ2 are complex numbers. If p is not zero, complex eigenvalues result in spiral trajectories. If p = 0, eigenvalues are purely imaginary and trajectories enclose the fixed point in ellipses or circles.
If p > 0 and q > 0 (the positive quadrant of the (q, p) plain), both eigenvalues have positive real parts (or are purely positive numbers), and the fixed point is unstable. If p > 0, and q = 0, one eigenvalue is positive and the other is zero: the trajectories are unstable lines.
Conversely, if p < 0 and q > 0 (the negative quadrant), both eigenvalues have negative real parts (or are purely negative numbers), and the fixed point is stable. If p < 0, and q = 0, one eigenvalue is negative and the other is zero: the trajectories are stable lines.
However, if q < 0, one eigenvalue is a positive number and the other is negative: trajectories follow the saddle point pattern.
|
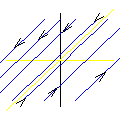
Finally, if p = 0 and q = 0 two possibilities exist. If A is the zero matrix, every vector x is an equilibrium point. If A is not the zero matrix, then µ1 = µ1 = 0 and a line of equilibrium points passes through the eigenvector corresponding to one zero eigenvalue. All other trajectories are parallel to this line, running in opposite directions on either side of the line of equilibrium points.
|
|
|