|
|
|
|
|
|
|
|
|
|








|
|
Egwald: Topics in Astronomy and Cosmology - Stellar Collapse
Egwald's popular web pages are provided without cost to users.
Modelling Stellar Collapse, Neutron Stars, and Black Holes Research Paper prepared for Kristin Schleich's Physics 407 course: Introduction to General Relativity (2018W). Abstract Stars that stop generating energy through nuclear fusion die. Smaller stars transform into white dwarf stars. Larger stars collapse to form neutron stars or black holes. Much larger stars may blow apart. Various coordinate transformations of the Schwarzschild metric are used to calculate geodesic trajectories of particles and radiation at various radii about stellar objects collapsing from self-gravitation. Within a black hole, the mechanics of stellar collapse are modelled with the geodesics of the Robertson-Walker metric (FLRW). I. Introduction Stars evolve by burning a sequence of lighter to heavier elements through the process of nucleosynthesis. Heavier elements are the result of the consumption of lighter elements. At each stage, the heaviest existing element accumulates in the core of the star, with lighter elements arranged in layers of decreasing atomic weight moving from the core to the surface of the star. High mass stars can burn through the entire sequence of hydrogen, helium, carbon, neon, oxygen, silicone, and iron. Because iron has the highest binding energy of all elements, this sequence of nucleosynthesis stops at iron. Thereafter, the outward pressure of the star’s hot gas cannot withstand the inward pull of gravity. Some other source of outward pressure is required to stop the star from collapsing through self-gravitation when energy production through fusion of lighter elements into heavier elements stops. The type of object that forms after a star collapses depends on its mass. Stars with a mass similar to the Sun's mass (M⨀), and up to 10 M⨀, wind up as white dwarf stars. After these stars blow off their outer layers as planetary nebulae, further gravitational collapse is prevented by electron degeneracy pressure. Larger stars form neutron stars or black holes when their iron cores collapse and they expend gravitational potential energy as supernovae. Electron and neutron degeneracy pressure are quantum mechanical, non-thermal sources of pressure. White dwarf and neutron stars within a binary system are able to increase their masses by accreting hydrogen from a close companion star. The maximum mass of a stable white-dwarf is 1.4 M⨀ - the Chandrasekhar limit. The maximum mass of a neutron star based on observations is 2.27 M⨀ - the Tolman-Oppenheimer-Volkoff limit. A white-dwarf that exceeds its mass limit will collapse into either a neutron star, a black hole, or shatter completely, producing a supernova. A neutron star that gets too large will collapse into a black hole and also create a supernova. The mass of a black hole is contained within a sphere, the event horizon, whose radius equals a parameter called the Schwarzschild radius. During stellar collapse to a black hole, a star's particles will either be expelled in a supernova or wind up inside the black hole. Once inside, a particle cannot leave a black hole since the escape speed from within the event horizon hole exceeds the speed of light. The ratio of the star's radius to its Schwarzschild radius for the neutron star PSR J0348+0432 in the constellation Taurus equals 2.2. The white dwarf supernova candidate, RX J0648.0-4418 in Puppis, has a ratio of 1500. For the supernova candidate Betelgeuse in Orion, it is 1.9 * 107. In geometric units with c = 1, and G = 1, the Schwarzschild radius equals twice the mass of the stellar object. A. The Schwarzschild Metric Albert Einstein's field equations of general relativity model the curvature of space-time in the vicinity of stellar objects [1]. Particularly, they relate the curvature of spacetime and the stress-energy from the presence of matter or other forms of energy. With certain simplifying assumptions, the Schwarzschild metric is a solution to these equations. In describing the gravitational field around the stellar object, the Schwarzschild metric and its transformations depend only on the mass of the object (M), the distance (r) to its center, the polar angle (θ), and the azimuthal angle (φ). Modeling spacetime within the framework of the Schwarzschild metric requires some fundamental assumptions. Schwarzschild spacetime is spherically symmetric in that there is no change after rotation around a chosen origin. Additionally, the metric is a vacuum solution to Einstein's field equations, with Ricci scalar R = 0. Furthermore, the Schwarszchild spacetime is static, which differs from the dynamic nature of the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric considered in Section C. For the purposes of this paper, Schwarzschild spacetime provides an approximate model of the collapse of a shell of dust that is infalling to a non-rotating stellar object. In solving for the geodesic equations of the Schwarzschild metric, the dθ/dτ component will be assumed to be zero constraining motion of particles to null geodesics, or particle freefall radial geodesics.
The Schwarzchild Metric Using the Schwarzschild metric given in Eqn. 1, the geodesic equations for a particle travelling in Schwarzschild geometry can be obtained. The derivation is omitted and the resulting first order terms for the general four-velocity of the metric are given below.
dt/dτ = ε / (1 - 2M/r) (2)
Here, the value of ε is set by the initial radial velocity at some time τ0 and the value of l is related to the angular momentum. With ε = 1 and l = 0 for radial infall of a particle from infinity, the following relationships between proper time τ, and r and coordinate time t are obtained [2]: r(τ) = (3/2)2/3 (2M)1/3(τ - τ) (5) where τ is the particle's final proper time at r = 0, and t(r) = t + 2M [-(2/3)(r/2M)3/2 - 2(r/2M)1/2 + ln| ( (r/2M)1/2 + 1 ) / ( (r/2M)1/2 - 1 )| ] (6) where the value of t selects a particular radial geodesic (see FIGS 2 and 3). The Schwarzschild metric has a coordinate singularity at r = 2M. This singularity can be removed by transforming the metric to more convenient coordinates. Let v = t + r* with dr* = dr / (1 - 2M/r). Integrating yields r* = r + 2M ln | (r/2M -1) | (7) Substituting dt = dv - dr* into the Schwarzschild metric results in the following version of the metric with Eddington-Finkelstein coordinates. 1. Eddington-Finkelstein Coordinates ds2 = -(1 - 2M/r) dv2 + 2dvdr + r2 (dθ2 + sin2(θ)dφ2) (8) The null geodesics are v = C1, and v = 2 * r* + C2, where C1 and C2 are different constants for each null geodesic trajectory.
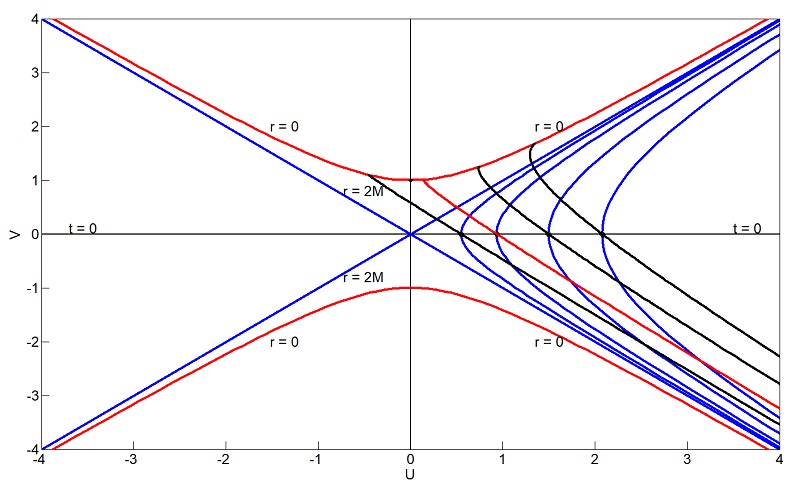
Matlab Program to generate Figure 1: Schwarzschild spacetime in Eddington-Finkelstein Coordinates. 2. Kruskal-Szekeres Coordinates A coordinate transformation into Kruskal-Szekeres coordinates extends the visible regions of spacetime allowing an observer to examine the behaviour of spacetime within a black hole, white hole, and theoretical alternate universes. Transforming Schwarzschild spacetime into Kruskal-Szekeres coordinates gives the resulting metric. ds2 = (32M3 / r) e-r/2M(-dV2 + dU2) + r2dΩ2 (9) subject to the constraints with which one can derive the Schwarzschild radius implicitly V2 - U2 = (1 - r/2M) er/2M (10) where the transformation is given by
V = √(r/2M - 1) er/4M sinh(t/4M) where Eqn. (11) is subject to r > 2M and Eqn. (12) subject to r < 2M.
Matlab Program to generate Figures 2 and 3: Schwarzschild spacetime in Kruskal-Szekeres Coordinates. B. Neutron Stars The Tolman-Oppenheimer-Volkoff limit describes the theoretical maximum stable mass of a neutron star before it will collapse into a black hole under its own gravity. Discussed in [3], an approximation was made by modeling the neutron star as a degenerate cold fermi gas. By assuming that the main source of energy within a star comes from thermonuclear reactions, one can model the neutron star as a collection of non-interacting fermions (neutrons). Above some critical mass, no stable configurations can be found for the fermi gas. This indicates that above some critical mass (the TOV limit), degeneracy is no longer strong enough to maintain the star's structure and the gas will collapse to a singular point - a black hole. The results from [3] resulted in a theoretical maximum of 0.7 M⨀, less than that of the Chandrasekhar limit which models the critical mass of a white dwarf. Through modelling the evolution of a neutron star from formation to a cold neutrino-free star, a different maximum value is obtained. Accounting for strong nuclear repulsion, [6] obtained a value closer to 2.27 M⨀. As this is the largest observed mass of a neutron star, this is presently set as the TOV limit. If a neutron star is under 2.27 M⨀, it can gain mass either through accretion of hydrogen from nearby companion stars, or the merger of two binary neutron stars can o ccur in which the sum of their masses exceed the TOV limit and the gravitational force dominates collapsing the star into a black hole. C. The Robertson Walker Metric The Friedmann-Lemaitre-Robertson-Walker (FLRW) metric is an exact solution of Einstein's field equations. A universe characterized by the FLRW metric is based on three assumptions. The first assumes that the space inside a FLRW universe is homogeneous. The universe is the same everywhere, but it is able to change as a function of time unlike a Schwarzschild universe. Additionally, the FLRW universe is spatially isotropic. There is no preferred direction of expansion or distribution of matter within the FLRW universe. Finally, the matter that is contained within the FLRW universe can be characterized solely by its pressure and density allowing one to solve for the equation of state and subsequent field equations from these two variables alone. The sign of the dimensionless, time-dependent a(t) factor is positive. While the universe is presently seen to be expanding, corresponding to an increasing value for a(t), regions of contracting spacetime, such as the collapse of a star into a black hole, correspond to a negative value for da/dt. The value of a(t) is determined by the Friedmann equation, a solution to Einstein's field equations [4], ((da(t)/dt)/a(t))2 = 8 π G ε(t) / (3c2) - κ c2 / (R02 a(t)2) (13) where ε(t) is the energy density, R0 is the radius of curvature, and possible values of κ are as below, along with the fluid equation and equation of state. The Robertson-Walker Metric ds2 = -dt2 + a(t)2(dr2 + Sκ2(r) (dθ2 + sin2(θ)dφ2) (14)
The value of Sκ(r) describes the curvature of spacetime, with radius of curvature of spacetime R, corresponding to positive, zero, and negative curvature respectively. D. Black Holes In order to study what would happen to observers as the process of entering a black hole from the surface or edge is `reversed', thereby beginning with the observer in the center of the black hole and moving outwards, requires a set of radial geodesics obtained from the FLRW metric.
d2t / dτ2 = -(a(t) da(t)/dt) / (1 - κ r2) * (dr / dτ)2
(16)
As an observer moves from the center of the black hole to the edge, which is impossible, but since the process is being `played back' it may be a valid thought experiment, time t becomes 'zero', and no longer spacelike. In the FLRW metric, time and proper time are the same. When radiation dominates over matter, as is the case inside a black hole, the expansion of the universe takes the form a(t) ∝ t1/2 [4].
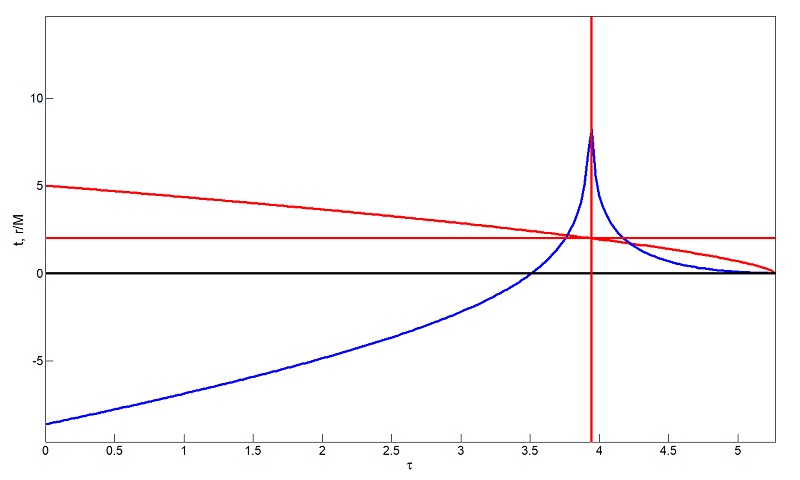
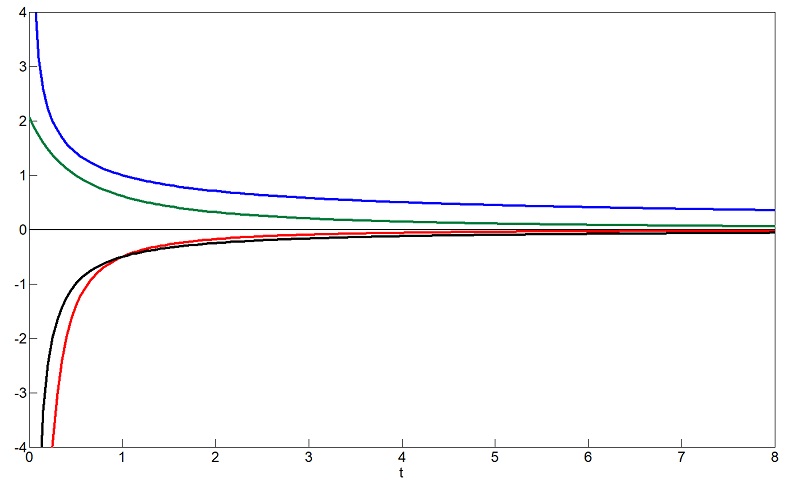
Another way of examining this process considers the scale factor a(t) to be proportional to t-1/2. Starting at time t = 0 and r = 2M, a photon will travel a path that increases rapidly, before slowing down. The scale factor is the inverse of the previous case, only this time modelled after a contracting universe. The result is the same, as the photon eventually approaches r = 0, with dr/dt = 0. The speed of light is a relationship between space and time, and at the center of a black hole, time becomes spacelike. Time 'blows' up to infinity, and if time is spacelike, the relationship between time and space, dr/dt, becomes 0. Fig. 4 shows a possible path of a photon inside a black hole, starting at t = 0 and r = 2M. Modelling the black hole similarly to blackbody photons in the early universe, and the processes inside the star as analogous to the big bang, the time-dependent relationship of temperature is given in Eqn. (18). T(t) ≈ 1010 K (t/1s)-1/2 (18) At t = 0, or at the edge of the black hole, the temperature diverges. In simpler terms, the temperature at the edge of the edge of the black hole is incredibly hot. At the center of the black hole, when t = ∞, the temperature is 0. This is comparable to the observation that super-massive black holes have a predicted temperature of 1.4 x 10-14 Kelvin, which is almost absolute zero. When an observer is drawn into a black hole, they are accelerated to nearly the speed of light. Their molecules collide much more rapidly, heating up to hundreds of millions of degrees Kelvin [5]. This also explains why when astronomers observe and try to measure the temperature of black holes, they record very high temperatures. They are actually observing the radiation from the observers or the material drawn in, masking the radiation escaping from the black hole itself. E. Discussion Modelling stellar collapse within the framework of general relativity is one way of predicting some of the properties of neutron stars and black holes. Schwarzschild spacetime is one of the simplest metrics to model black holes, but assumes no Hawking radiation, charge, or rotation. The FLRW metric assumes isotropy and homogeneity in the universe where matter is equally distributed. By deriving the geodesics of the FLRW metric, the path a photon travels in a black hole, assuming radiation dominance, can be investigated. The scale factor in the equation is dependent on the equation of state. A more accurate understanding of the equations of state for neutron stars could cement an experimental value for the TOV limit, using more suitable spacetime metrics. F. References
[1] Einstein A. Die Grundlage der allgemeinen Relativitätstheorie. Annalen der Physik. 1916; 354(7):769-822.
|
|