| |
Egwald: Topics in Astronomy and Cosmology - Gravitational Lensing
by
Elmer G. Wiens
Egwald's popular web pages are provided without cost to users.
Follow Elmer Wiens on Twitter:

Gravitational Lensing

Introduction
Gravitational lensing refers to the perceived influence of a celestial object's gravity on light passing by the object. The object's
mass bends spacetime, bending light's path, and focusing its measured brightness. As predicted by Einstein's Theory of General Relativity,
the foreground object acting as a lens may generate multiple images or ring-images of the background object's emitted light.
Angle of Deflection / Impact Parameter
Einstein predicted that an object with compact mass, M, would deflect a ray of light passing by the object at a distance, b, by an angle, α, given by the formule:
1) α = 4 *G * M / (b * c2),
where G = gravitational constant and c = speed of light.
The angle α is called the angle of deflection; the distance b is called the impact paramer.
Geometry of Gravitational Lensing.
|
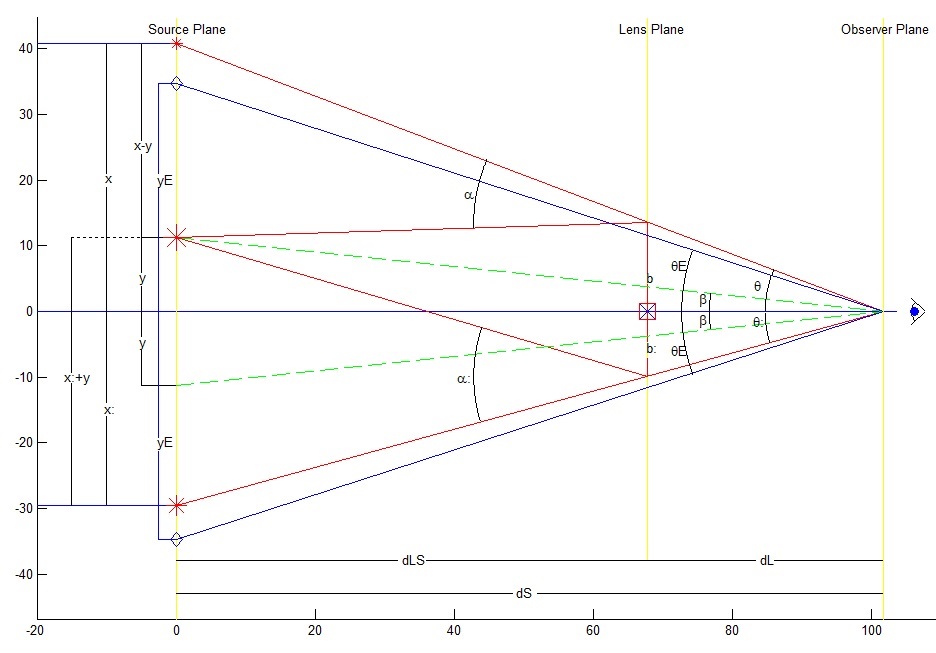
Figure 1
|
In the diagram above, the observer and the lens object lie along the X axis. The source object is assumed to lie above the X axis along the Y axis. The
source object (the large star) lies between the two perceived images (the two smaller stars).
The gravity of the object in the lens plane at a distance dLS from the source bends the ray of light. The observer, at a distance dS from the source,
and dL from the lens, sees the middle image deflected by an angle α to top image, and at an angle α: to the bottom image. The distance from the top
image to the X axis is x units; the distance from the bottom image to the X axis is x: units; the source object itself lies y units above the X axis.
It is assumed that the mass of the lens is concentrated at a single point, and that the distances are great enough to approximate the hyperbolic paths of rays
of light from the source to the observer by straight lines.
With the mass of the lens contained in a small volume, the lens will produce two images, unless the source image lies along the line of sight of the observer and
the lens, in which case a ring appears (Einstein Ring).
Replicating Figure 1.
To replicate Figure 1, let the mass of the lens object MLens = MMW = 1022 * MSun kg, and α = 25 * π / 180 radians.
From equation 1) b = 4 * G * MLens / (c2 * α) = 1.36e+26 meters. Let x = 3 * b = 4.083e+26 m.
Let θ = 23 * π /180 radians, then dS = x / θ = 1.0173e+27 m, dL = dS / 3 = 3.391e+26 m, dLS = dS – dL = 6.782e+26 m.
(Using the angular diameter distance over cosmological distances dS + dL ≠ dS)
Also, y = x – dLS * α = 1.1245e+26 m, and the angle β = y / dS. Now scale all distances by dividing by 1025 meters.
Justification of Figure 1.
First, consider the top half of the diagram.
Assuming that b << dL << dS, θ = b / dL = x / dS → b = x * dL / dS, and α = (x – y) / dLS.
From equation 1), α = 4 *G * M / (c2 * b) = (x – y) / dLS → x – y = (4 * G * M / c2) * (dLS * dS / dL) * (1 / x),
→ x2 - y * x = (4 * G * M / c2) * (dLS * dS / dL) = yE2 by definition;
2) → x2 - y * x - yE2 = 0,
3) → x = (y + √(y2 + 4 * yE2))/2, since x > 0.
Second, consider the bottom half of the diagram.
Again assuming that b: << dL << dS, θ: = b: / dL = x: / dS → b = x: * dL / dS, and α: = (x: + y) / dLS.
From equation 1), α: = 4 *G * M / (c2 * b:) = (x: + y) / dLS → x: + y = (4 * G * M / c2) * (dLS * dS / dL) * (1 / x:),
→ x:2 + y * x: = (4 * G * M / c2) * (dLS * dS / dL) = yE2 by definition;
4) → x:2 + y * x: - yE2 = 0,
5) → x: = (-y + √(y2 + 4 * yE2))/2, since x: > 0.
Subtracting 4) from 2),
6) x – x: = y, → x - y = x:, x: + y = x.
Making the necessary substitutions,
7) α = x: / dLS, α: = x / dLS.
So, the angle of deflection, α, equals the ratio of the distance the lower image lies below the X axis to the distance of the lens object form the source object. The angle of
deflection, α:, equals the ratio of the distance the upper image lies above the X axis to the distance of the lens object form the source object.
8) θ = b / dL = x / dS, θ: = b: / dL = x: / dS → θ > θ:
If the source object lies on the X axis, → y = 0, and x = yE = x:
The Einstein angular radius θE.
θE = yE / dS = [ (4 * G * M / c2) * (dLS * dS / dL) *(1 / dS2) ](1/2)
9) → θE = [ (4 * G * M / c2) * dLS / (dL * dS) ](1/2), definition.
Then, x > yE → θ > θE; x: < yE → θ: < θE
10) → θ > θE > θ:
In words, the image farthest from the line of sight between the observer and the lens object is located at a greater angle from the X axis than the Einstein angular
radius, while the image closest to the line of sight between the observer and the lens object is located at a smaller angle from the X axis than the Einstein angular radius.
Magnification of the source image by the gravitational lens.
In the following analysis I will show that the image closer to the source object is dimmer than the image farther from the source.
The magnification of an image by the lens is defined as the ratio of the solid angle of the image to the solid angle of the source
(Solid Angle).
11) A = θ dθ / β dβ, definition.
First, consider the closer image to the source object.
From equation 2), 1 – y / x = yE2 / x2 = (θE * dS / θ dS)2 = (θE / θ)2.
12) → y / x = 1 – (θE / θ)2 → x / y = (1 – (θE / θ)2)-1
Also, x2 – y * x = yE2 → x – y = yE2 / x → dx – dy = -(dx/x2) * yE2
So, 1 – dy / dx = (yE / x)2 = (θE / θ)2
13) → dy / dx = 1 + (θE / θ)2 → dx / dy = (1 + (θE / θ)2)-1
Since, θ = x / dS, β = y / dS; dθ = dx / dS, dβ = dy / dS ... (notation: dS ≠ deferential of S)
Substituting into equation 11),
A = θ dθ / β dβ = ( x dx / y dy) = (1 – (θE / θ)2)-1 * (1 + (θE / θ)2)-1
14) → A = (1 – (θE / θ)4)-1.
Similarly, with the image below the X axis.
From equation 4) 1 + y / x: = yE2/x:2 = (θE * dS / θ: dS)2 = (θE / θ:)2
15) → y / x: = -1 + (θE / θ:)2 → x: / y = (-1) * (1 – (θE / θ:)2)-1
Also, x:2 + y * x: = yE2 → x: + y = yE2 / x: → dx: + dy = -(dx: / x:2) * yE2
So, 1 + dy / dx: = -(yE / x:)2 = -(θE / θ:)2
16) → dy / dx: = (-1) * (1 + (θE / θ:)2) → dx: / dy = (-1) * (1 + (θE / θ:)2)-1
Since, θ: = x: / dS, β = y / dS; dθ: = dx: / dS, dβ = dy / dS (notation: dS ≠ deferential of S)
Substituting into equation 11),
A: = θ: dθ: / β dβ = ( x: dx: / y dy) = (-1)2 * (1 – (θE / θ:)2)-1 * (1 + (θE / θ:)2)-1
17) → A: = (1 – (θE / θ:)4 )-1
Therefore, since θ > θE > θ:
18) A: > A
In words, the magnification of the image farther from the source is greater than the magnification of the image closer to the source. Consequently, in Figure 1 the
deflected image below the line of sight is brighter than the deflected image above the line of sight.
References
Astronomy. "Weird Object: The Einstein cross." http://astronomy.com/magazine/weirdest-objects/2015/09/15-the-einstein-cross
Hickson, Paul (2016). Astronomy 300. Galaxies. Univesity of British Columbia Course Notes.
Sparke, L. S. and J.S. Gallagher, III (2007). Galaxies in the Universe. (2nd ed.). Cambridge: Cambridge UP.
Wambsganss, Joachim (1998). “Gravitational Lensing in Astronomy.” Springer Links. https://link.springer.com/article/10.12942%2Flrr-1998-12.
|
|